1.3 有符号的二进制数

一般来说，我们用没有符号表示的数来表示正数（无符号数），而用“减号”（负号）表示负数。然而，这些表示方法并不适用于像计算机这样的数字系统，因为数据是以二进制数表示的。因此，需要一种特殊的表示法来表示符号。

正数的二进制表示

最高有效位（MSB）为0的二进制数称为“正数的二进制数”。

负数的二进制表示

最高有效位（MSB）为1的二进制数称为“负数的二进制数”。

无符号数可以有很宽的表示范围。然而，对于有符号数，其表示范围只能从 $- (2^{(n-1)} - 1)$ 到 $+ (2^{(n-1)} - 1)$，其中 $n$ 是位数（包括符号位）。

例如，对于一个5位有符号二进制数（包括4位数值位和1位符号位），其范围为：

$- (2^{(5-1)} - 1) \text{ 到 } + (2^{(5-1)} - 1)$ $-(2^{4} - 1 ) \text{ 到 } + (2^{4} - 1)$ $-15 \text{ 到 } +15$

8位无符号二进制数的范围为0到255。8位有符号二进制数的最大值和最小值如下所示。

最大正数为：0111 1111，即 $+127$

最大负数为：1000 0000，即 $-127$

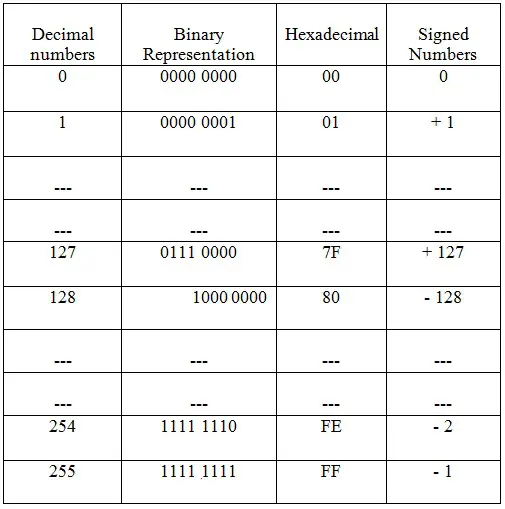
由于我们不能将正负号输入到数字系统中，因此需要用其他方式来表示这些符号。在计算机中，表示负数有三种常见方法，分别是：

• 符号-数值表示法
• 1的补码表示法
• 2的补码表示法

符号-数值表示法

可以通过最高有效位（MSB）来判断二进制数是正数还是负数的数称为“有符号二进制数”。

例如：1001 → +9（正数）；1 001 → –1（负数）

这是在二进制系统中表示正数和负数的最简单方法。在符号-数值表示法中：

• 正数用其最高有效位（MSB）为‘0’来表示。
• 负数用其最高有效位（MSB）为‘1’来表示。

1的补码表示法

1的补码是另一种将负二进制数输入到计算机中的方法。在1的补码方法中，正二进制数保持不变，而负数则通过对无符号正数取1的补码来表示。

正数的最高有效位（MSB）始终为0，而负数的最高有效位（MSB）始终为1。

1的补码是通过将所有0替换为1，将所有1替换为0来生成的。

例如，如果一个二进制数是01101001，那么它的1的补码是10010110。

让我们再来看一些关于1的补码的例子。

例1：$-33 = ?$

33的二进制表示为 $100001_2$

在8位表示法中，它表示为 $0010 0001_2$

现在，-33用1的补码表示为 $1101 1110_2$

例2：$-127 = ?$

在8位表示法中，127表示为 $0111 1111_2$

现在，-127用1的补码表示为 $1000 0000_2$

例3：$-1 = ?$

1的二进制表示为 $001_2$

在8位表示法中，它表示为 $0000 0001_2$

现在，-1用1的补码表示为 $1111 1110_2$

使用反相器求1的补码

对于数字电子电路来说，求一个数的1的补码的最简单方法是使用“反相器”。顾名思义，反相器是一种设备/电路，它生成输入的补码。

反相器并联连接，以获得输入二进制数的1的补码。无论一个二进制数有多少位数字，我们都可以很容易地找到它的1的补码。只需将所有的0写成1，将所有的1写成0，就可以得到一个二进制数的1的补码。

在二进制数上进行的数学运算称为“二进制算术”。我们可以通过多种方式对任何正数或负数进行加法或减法运算，例如 $A + B$、$A + (-B)$、$-B + A$ 等。

有符号二进制数的加法

二进制加法也遵循与普通加法相同的规则。但这里唯一的例外是，数学运算只在两个数字（0和1）之间进行，且始终有 $1 > 0$。

二进制加法的规则如下：

使用1的补码进行减法

要从另一个二进制数中减去一个数，首先需要将其转换为其1的补码。

使用1的补码进行负数减法运算有以下3种可能的情况。

情况1：负数小于正数。

例如：$(28)_{10}$ 和 $(-15)_{10}$

我们知道28在二进制数系统中表示为 $011100_2$

15在二进制数系统中表示为 $01111_2$

15的1的补码是 $10000_2$，即 $-15$

结果为 $(13)_{10}$，在二进制系统中表示为 $0 01101$

情况2：负数大于正数。

例如：$(-28)_{10}$ 和 $(15)_{10}$

我们知道28在二进制数系统中表示为 $011100_2$

15在二进制数系统中表示为 $01111_2$

28的1的补码是 $100011_2$，即 $-28$

结果为 $(-13)_{10}$，在二进制系统中表示为 $1 10010$

情况3：两个数都是负数。

例如：$(-28)_{10}$ 和 $(-15)_{10}$

我们知道28在二进制数系统中表示为 $011100_2$

28的1的补码是 $100011_2$，即 $-28$

15在二进制数系统中表示为 $01111_2$

15的1的补码是 $10000_2$，即 $-15$

结果为 $(-43)_{10}$，在二进制系统中表示为 $1010100$

有符号二进制数的2的补码
求2的补码的过程类似于求十进制数的10的补码的过程。要找到一个二进制数的2的补码，首先需要找到该数的1的补码，然后在1的补码上加“1”。

正数的2的补码表示与1的补码和符号-数值表示相同。

求2的补码涉及以下两个步骤：

步骤1：求1的补码

步骤2：在无符号数结果上加“1”

让我们通过一些例子来理解这一点。

例1：$-33 = ?$

33的二进制表示为 $100001_2$

在8位表示法中，它表示为 $0010 0001_2$

现在，-33用1的补码表示为 $1101 1110_2$

加上1（0000 0001），结果为 $1101 1111_2$

因此，-33的2的补码是 $1101 1111_2$

例2：$-127 = ?$

在8位表示法中，127表示为 $(0111\ 1111)_2$。

现在，-127用1的补码表示为 $(1000\ 0000)_2$。

加上1 $(0000\ 0001)_2$ 后，

结果为 $(1000\ 0001)_2$。

因此，-127的2的补码是 $(1000\ 0001)_2$。

例3：$-1 = ?$

1表示为 $(001)_2$。

在8位表示法中，它表示为 $(0000\ 0001)_2$。

现在，-1用1的补码表示为 $(1111\ 1110)_2$。

加上1 $(0000\ 0001)_2$ 后，

结果为 $(1111\ 1111)_2$。

因此，-1的2的补码是 $(1111\ 1111)_2$。

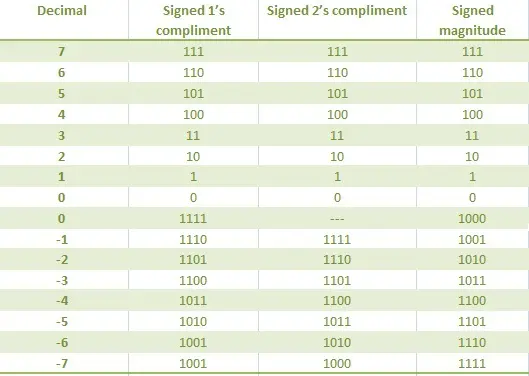
有符号二进制数总结

可以通过最高有效位（MSB）来识别的二进制数称为“有符号二进制数”。

如果MSB为1，则为“负有符号二进制数”。例如：$-1 = 1001$。

如果MSB为0，则为“正有符号二进制数”。例如：$+9 = 0001$。

计算机无法理解减号。因此，为了将负数输入到计算机中，我们采用以下3种特殊方法：

• 符号-数值表示法
• 1的补码表示法
• 2的补码表示法

1的补码表示为“将所有的1替换为0，将所有的0替换为1”。

例如：15的1的补码，即 $-15$，表示为 $(10000)_2$，即 $-15$。

2的补码表示为“在所需数的1的补码上加1”。

例如：-33的2的补码是 $(1101\ 1111)_2$。

二进制数的加法和减法等数学运算称为“二进制算术运算”。